Arriba temos tres exemplos de representacións de figuras humanas en distintos materiais, de culturas e épocas diferentes:
unha venus paleolítica: a Venus de Willendorf (20 000 a.C.)
un fragmento do mosaico da arpa das tumbas reais de Ur (2400 a.C.)
un arpista da arte cicládica (3000-2000 a.C.)
Volve miralas, ¿cres que son proporcionadas, que responden a un modelo, que imitan a realidade?, ¿parécenche fermosas?. En cada caso vemos desproporcións: a venus semella excesivamente obesa e cunhas extremidades mínimas; no seguinte caso, se as figuras fosen naturalistas, teríamos un xigante sentado; e ¿que dis dos brazos do arpista?.
Así comezaron as representacións da figura humana, houbo de pasar un tempo para que o modelo entrara nas inquedanzas teóricas dos artistas, entendendo que a beleza non só é unha calidade do obxecto senón que tamén ten que ver a psique do suxeito que observa, o que nos levaría a outro tema. a formación estética.
A idea era conseguir a beleza por métodos obxectivos servíndose da xeometría e do número. Para iso era preciso establecer un sistema de proporcións para unha figura ideal, e deste presuposto derivan os tres conceptos que tratamos referidos á representación artística:
Ó longo da historia formuláronse diferentes propostas que son as que vamos revisar.
1- MÓDULO EXIPCIO
A partir dunhas cuadrículas atopadas sobre pinturas inacabadas nunha tumba de Sakkara da época de Zoser e, posteriormente, tamén en papiros, concluíuse que era a planificación de proporcións para facer as figuras. As distintas partes do corpo adáptanse ós cadrados da retícula servindo ademais para poder adecuarse a calquera escala.
Este canon clásico de 18 puños mantívose moito tempo pero finalmente, a partir da dinastía XXVI, foi alongado pasando a un canon de 21 puños. Compara a diferencia na imaxe da esquerda, agora o canon é moito máis estilizado.
Como a arte exipcia representa o constante, o inmutable, a forma queda estereotipada. Nin sequera o movemento é orgánico senón puramente mecánico, é dicir só hai cambio na posición dun elemento pero ese cambio non repercute nos restantes.
Na imaxe da esquerda temos dúas figuras en movemento -4 1/2 ou 5 1/2 cuadrículas da punta dun pé á punta do outro-, e unha ten o brazo levantado, ¿cambio algo na súa representación?, nada cambia: o artista constrúe unha imaxe significativa e simbólica sen intentar imitar a realidade.
Leocares xa no século IV a.C., mantén a cabeza como módulo prolongando o canon ata 8 cabezas e media. Así o reflicte o Apolo Belvedere, unha figura en movemento, copia romana dun orixinal en bronce atribuído a Leocares
3- ROMA CONTINÚA O ESTUDIO DO CANON
...
- Vitruvio scripsit
Este arquitecto romano do século I a.C., só fixo unha obra pero escribiu o tratado De Architectura, 10 libros dedicados a Augusto nos que analiza tanto a parte teórica coma a parte edilicia da arquitectura.
Se xa vimos como explica a orixe das cariátides, agora imos fixarnos na súa exposición sobre a compositio, sexa de elementos arquitectónicos -basas, capiteis,...- ou sexa da figura humana. Entende por compositio a planificación dun sistema de proporcións tendo como referente un módulo, nos templos sería a súa anchura que ven dada do diámetro da columna, equivalente a un pé. Columna que por certo se constrúe a imitación do home: a basa é o pé, o fuste será o corpo e o capital equivale á cabeza.
Pero deixemos a arquitectura e vaiamos ó canon da figura humana para configurar o homo bene figuratus. Os membros do corpo son partes proporcionadas do todo e mídense por medio dunha unidade mínima -e as súas fraccións- que pode ser o palmo ou o dedo, xa que 4 palmos ou 16 dedos forman a dimensión dun pé, a unidade básica dos romanos.
A altura proporcionada é a correspondente a 24 palmos, 96 dedos ou 6 pés, pero tamén 8 cabezas, o mesmo que no canon de Lisipo, ou 10 rostros. Así dice:
Certamente as propostas de Vitruvio tiveron fonda influencia tanto na Idade Media como, especialmente, no Renacemento.
5- O MUNDO MEDIEVAL
...
A perda dos coñecementos clásicos e o teocentrismo fixeron que as reflexións teóricas escasearan nesta longa etapa e que os mestres se despreocuparan das proporcións perfectas da figura humana. A concepción simbólica da arte fai que se busque a beleza ética e non tanto a beleza estética.
Desde un románico caracterizado pola rixidez e planitude pasamos, a partir do século XII, ó gótico que alonga e estiliza as figuras ó tempo que as humaniza, pero en ningún caso se chega a establecer un módulo ou un canon, cada artista interpreta libremente as proporcións.
Reflexións teóricas sobre a beleza só as encontramos en san Agustín quen continuando coa tradición clásica a fundamenta na medida, a proporción e o ritmo.
- Villard de Honnecourt, mestre arquitecto do século XIII escribiu Livre de portraiture, unha especie de caderno de viaxe -os mestres eran itinerantes- con debuxos e explicacións de todo o que considera de interese sobre técnicas construtivas, deseños de máquinas, métodos para representar figuras humanas. Sérvese de formas xeométricas sinxelas -triángulos, cadrados, rectángulos- sen chegar a integrar un completo sistema de proporcións, aínda que se aproxima: divide a altura total en 7 partes.
Triangulación e segmentación con liñas de guía, serven tanto para as figuras estáticas como en movemento.
Será a unidade de medida que igualmente seleccione Diego de Sagredo, arquitecto español que publica en 1565 Medidas do Romano, a primeira versión dialogada fora de Italia sobre Vitruvio.
6- A ITALIA DO RENACEMENTO
A Italia renacentista retomou o estudio dos sistemas de proporcións con verdadeira veneración, entendéndoas como a realización dun postulado metafísico, non como un mero procedemento técnico. Só Alberti e Leonardo adentráronse pola senda do empirismo na procura dunha antropometría verdadeiramente científica.
- Leon Battista Alberti -matemático, poeta, arquitecto, erudito,..- retoma o estudio das proporcións. En De pictura (1435) escribe sobre a necesidade de valerse da observación e a necesidade da proporción
Este modelo canónico de medición precisa variacións para adecuarse a casos particulares. Neste sentido alude á fábula de Zeuxis (pintor grego do século V a.C.) quen para representar a Helena de Troia pregou ás cinco doncelas máis fermosas de Crotona que lle permitiran pintar o mellor de cada unha.
¿Como modificar entón o modelo? Para cambiar as proporcións crea o definitor, un instrumento de medición no que se xoga coa lonxitude do exempeda -a regla de 6 pés, subdivididos en 60 polgadas e 600 minuta-, sistema de medidas por el creado, que tiña como vantaxe empregar unidades moito mais pequena que a cabeza, o rostro ou o pé.
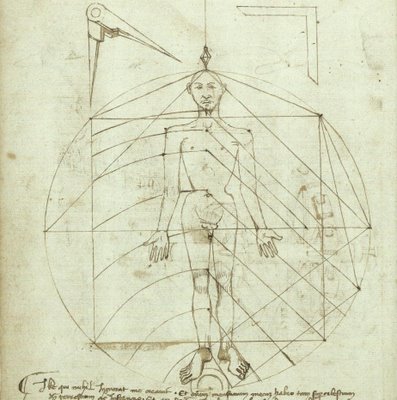
- Leonardo da Vinci, partindo das proporcións sinaladas por Vitruvio, elabora sobre 1490 un debuxo no que aplica os principios vitruvianos sobre as proporcións do corpo humano. Pero fixo algunha corrección como considerar o pé a sétima parte da altura.
Así comezaron as representacións da figura humana, houbo de pasar un tempo para que o modelo entrara nas inquedanzas teóricas dos artistas, entendendo que a beleza non só é unha calidade do obxecto senón que tamén ten que ver a psique do suxeito que observa, o que nos levaría a outro tema. a formación estética.
A idea era conseguir a beleza por métodos obxectivos servíndose da xeometría e do número. Para iso era preciso establecer un sistema de proporcións para unha figura ideal, e deste presuposto derivan os tres conceptos que tratamos referidos á representación artística:
canon, sería a regra ou precepto a seguir, un sistema de medidas
módulo, será a medida fundamental, a unidade de medida base (cabeza, pé, palmo)
proporción, sería a relación correcta das partes entre si e das partes có todo
Ó longo da historia formuláronse diferentes propostas que son as que vamos revisar.
1- MÓDULO EXIPCIO
..
A arte exipcia foi a primeira en empregar un sistema racional de proporcións por medio dun sistema reticular que impoñía formas xeométricas ás figuras. O modelo convértese nunha norma que facilita a execución escultórica ou pictórica.
A arte exipcia foi a primeira en empregar un sistema racional de proporcións por medio dun sistema reticular que impoñía formas xeométricas ás figuras. O modelo convértese nunha norma que facilita a execución escultórica ou pictórica.
 |
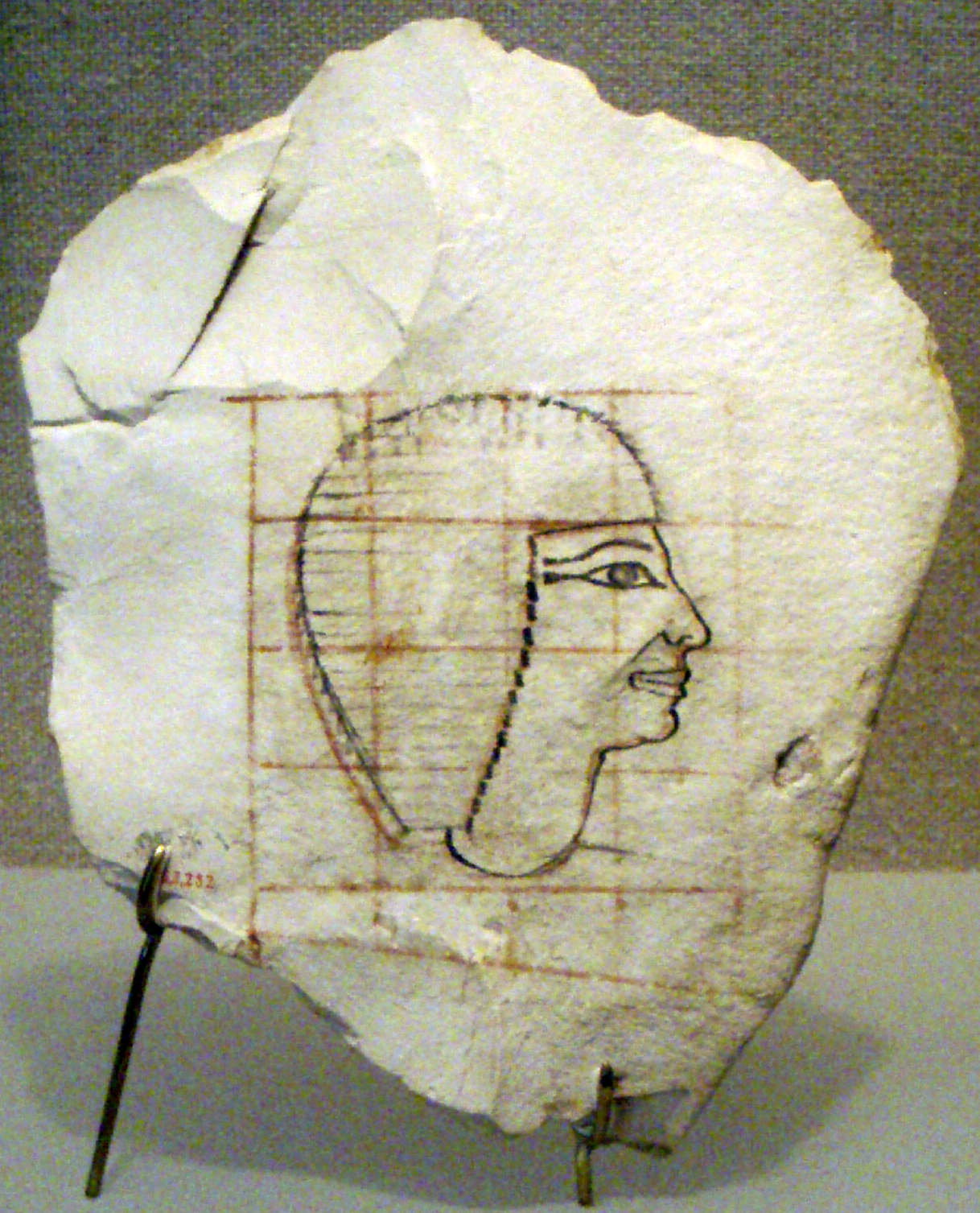| Ostracon Senenmut |
Os primeiros sistemas foron aínda máis sinxelos, unha liña vertical dividía o corpo en dúas metades mentres que verticalmente se dividía en tres partes, tres partes que seguiron manténdose cando se pasou a empregar o engrellado.
A unidade base, o módulo, era o puño -anchura da palma da man na dobra central- que coincide cun cadrado da cuadrícula e que equivale a un terzo do pé.
Pero tamén outras dúas unidades: o cóbado, ou cúbito, pequeno e o cóbado, ou cúbito, real. O primeiro é a lonxitude desde o interior do cóbado pero chega ata o polgar, sempre coa man estendida; corresponde a 4 cuadrículas e media; o segundo vai tamén desde o interior do cóbado ata o dedo corazón coa man estendida (5 cuadrículas e cuarto).
Consideraron figura de perfecta beleza aquela de 18 puños de altura, desde a planta do pé ata a liña do pelo: 2 puños para a cabeza -ata o arranque do pelo-, 10 puños para o corpo -dos ombreiros ós xeonllos- e 6 puños para as pernas desde os xeonllos. Para as figuras sentadas adoptouse un canon de 14 puños.
A fórmula chegou a estandarizarse tanto que, se ben unhas liñas non eran significativas, outras o eran moito, tal e como ves abaixo.
 |  |
A fórmula chegou a estandarizarse tanto que, se ben unhas liñas non eran significativas, outras o eran moito, tal e como ves abaixo.
Este canon clásico de 18 puños mantívose moito tempo pero finalmente, a partir da dinastía XXVI, foi alongado pasando a un canon de 21 puños. Compara a diferencia na imaxe da esquerda, agora o canon é moito máis estilizado. Como a arte exipcia representa o constante, o inmutable, a forma queda estereotipada. Nin sequera o movemento é orgánico senón puramente mecánico, é dicir só hai cambio na posición dun elemento pero ese cambio non repercute nos restantes.
Na imaxe da esquerda temos dúas figuras en movemento -4 1/2 ou 5 1/2 cuadrículas da punta dun pé á punta do outro-, e unha ten o brazo levantado, ¿cambio algo na súa representación?, nada cambia: o artista constrúe unha imaxe significativa e simbólica sen intentar imitar a realidade.
Con estas formulacións técnicas tan precisas, sen ter en conta a percepción, a obra artística resulta sempre idéntica independentemente de quen sexa o seu autor, pois todos traballan sobre a mesma formulación sen procurar un estilo persoal. Tal homoxeneidade é un trazo característico da arte exipcia.
2- NA ARTE GREGA
..
As preocupacións teóricas sobre as proporcións foron un tema recorrente no mundo grego, moi interesado nas relacións numéricas e nas matemáticas para explicar os fenómenos naturais e tamén a beleza.
Tomemos como punto de partida este comentario de Platón
Paralelamente os gregos introducen un cambio de grande importancia: abandonar a rixidez estándar do canon exipcio que aínda utilizaron no período arcaico (kouroi e korai).
- Policleto e o Κανών
As cousas cambiaron pouco a pouco a medida que se percorría o camiño a prol da naturalidade. Fundamentais foron os coñecementos anatómicos que se podían realizar a través da observación dos atletas que corrían espidos -o estudio de cadáveres estaba prohibido- e as reflexións filosóficas, ó que habería que sumar a capacidade dedutiva e o dominio técnico do artista.
A estética clásica presupoñía que había unha beleza obxectiva, entendida beleza como harmonía, e unhas proporcións igualmente obxectivas coas que acadala. Pero non se tratará dun sistema ríxido de carácter técnico, o artista terá en conta as variacións anatómicas, o punto de vista, a distancia,... pois o resultado ha ser esteticamente relevante.
No Canon, un tratado teórico practicamente perdido, Policleto (segunda metade do s. V a.C.) céntrase na composición escultórica e na relación entre as partes do corpo humano para acadar deste xeito a beleza, que, insistimos, os gregos consideraban fundamentada nas relacións numéricas, de novo a influencia dos pitagóricos: a proporción coma a orde divina, nada queda ó azar e todo está rexido polas matemáticas.
E así Policleto o plasmou no Dorífero (unha obra que estudamos), escultura en bronce só coñecida por copias romanas en mármore: unha figura masculina cun corpo dunha proporción conmensurable de números enteiros: como módulo, a cabeza, e cunha altura de 7 cabezas.
Sen embargo como ves no texto anterior tamén emprega como unidade de medida o palmo -anchura dos catro dedos- o que recorda a formulación exipcia. Policleto non pretende servirse dun único módulo senón que expresa a medida da parte máis pequena como fracción dunha maior.
Isto di Plinio o Vello, admirando a obra do broncista:
- Modificando o canon
Eufránor de Corinto, recoñecido tanto na escultura coma na pintura, escribiu un importante tratado De Symmetria et Coloribus. Sérvese dunhas proporcións que fan das súas esculturas figuras de longos e delgados corpos, grandes cabezas e grosas articulacións, de xeito que súa modificación do canon de Policleto non logrou acadar unhas proporcións gráciles, así polo menos o critica Plinio.
Lisipo procurou igualmente un arquetipo da figura humana, pero cunha visión subxectiva, de xeito que a beleza hase plasmar en formas que teñan en conta a visión humana. El mesmo dixo, de novo segundo Plinio:
..
As preocupacións teóricas sobre as proporcións foron un tema recorrente no mundo grego, moi interesado nas relacións numéricas e nas matemáticas para explicar os fenómenos naturais e tamén a beleza.
Tomemos como punto de partida este comentario de Platón
[...] é imposible combinar dúas cousas sen unha terceira: é preciso que exista entre elas un vínculo que as una. Non hai mellor vínculo que o que fai de si mesmo e das cousas que une un todo único e idéntico. Agora ben, tal é a natureza da proporción [...]
PLATON, Timeo, 31cO seu punto de partida é a harmonía das proporcións, entendendo que proporción equivale a simetría, non no sentido actual de equidistancia respecto dun eixo ou centro, senón no sentido de relación entre as partes e destas co todo.
Paralelamente os gregos introducen un cambio de grande importancia: abandonar a rixidez estándar do canon exipcio que aínda utilizaron no período arcaico (kouroi e korai).
- Policleto e o Κανών
As cousas cambiaron pouco a pouco a medida que se percorría o camiño a prol da naturalidade. Fundamentais foron os coñecementos anatómicos que se podían realizar a través da observación dos atletas que corrían espidos -o estudio de cadáveres estaba prohibido- e as reflexións filosóficas, ó que habería que sumar a capacidade dedutiva e o dominio técnico do artista.A estética clásica presupoñía que había unha beleza obxectiva, entendida beleza como harmonía, e unhas proporcións igualmente obxectivas coas que acadala. Pero non se tratará dun sistema ríxido de carácter técnico, o artista terá en conta as variacións anatómicas, o punto de vista, a distancia,... pois o resultado ha ser esteticamente relevante.
No Canon, un tratado teórico practicamente perdido, Policleto (segunda metade do s. V a.C.) céntrase na composición escultórica e na relación entre as partes do corpo humano para acadar deste xeito a beleza, que, insistimos, os gregos consideraban fundamentada nas relacións numéricas, de novo a influencia dos pitagóricos: a proporción coma a orde divina, nada queda ó azar e todo está rexido polas matemáticas.
Un corpo perfecto habería de ser harmónico, simétrico e proporcionado, e para logralo di: a perfección nace pouco a pouco por medio de moitos cálculos.
O pouco que sabemos dos principios de Policleto son os recollidos polo médico Galeno (s.II d.C.) no seu texto De temperamentis. En forma dialogada escribe
... Pensa que a beleza non está na simetría dos elementos, senón das partes, é dicir, dun dedo en relación a un dedo, de todos eles en relación ó cóbado, do cóbado en relación ó brazo e de todo en relación ó todo, segundo está escrito no Canon de Policleto. Pois tras de ensinarnos naquel libro todas as simetrías do corpo, Policleto confirmou de feito a súa teoría ó facer unha estatua segundo o prescrito pola súa teoría e chamala, precisamente tamén á propia estatua como o libro, Canon.
É necesario -afirma Polícleto- que a cabeza sexa a sétima parte da altura total da figura, o pé dúas veces a lonxitude da palma da man mentres a perna, desde o pé ao xeonllo, deberá medir seis palmos, e a mesma medida haberá tamén entre o xeonllo e o centro do abdome. Para demostrar a exactitude do seu canon esculpiu unha estatua que nos chegou en numerosas copias romanas: o Doríforo -é dicir, o portador de lanza-, un mozo, unha vez máis, completamente espido, que leva con desenvoltura unha lixeira lanza na man.
E así Policleto o plasmou no Dorífero (unha obra que estudamos), escultura en bronce só coñecida por copias romanas en mármore: unha figura masculina cun corpo dunha proporción conmensurable de números enteiros: como módulo, a cabeza, e cunha altura de 7 cabezas. Sen embargo como ves no texto anterior tamén emprega como unidade de medida o palmo -anchura dos catro dedos- o que recorda a formulación exipcia. Policleto non pretende servirse dun único módulo senón que expresa a medida da parte máis pequena como fracción dunha maior.
Isto di Plinio o Vello, admirando a obra do broncista:
Policleto incorporou toda a arte nunha soa obra
- Modificando o canon
Eufránor de Corinto, recoñecido tanto na escultura coma na pintura, escribiu un importante tratado De Symmetria et Coloribus. Sérvese dunhas proporcións que fan das súas esculturas figuras de longos e delgados corpos, grandes cabezas e grosas articulacións, de xeito que súa modificación do canon de Policleto non logrou acadar unhas proporcións gráciles, así polo menos o critica Plinio.
Lisipo procurou igualmente un arquetipo da figura humana, pero cunha visión subxectiva, de xeito que a beleza hase plasmar en formas que teñan en conta a visión humana. El mesmo dixo, de novo segundo Plinio:
Ata agora representáronse os homes como son, en cambio, eu os represento como me parecen
Estiliza as figuras ó prolongar a súa altura mantendo como unidade de medida a cabeza. Se o canon de Policleto era de 7 cabezas, uns cen anos despois Lisipo pasa a 8 cabezas (análise do Apoxiómenos), ou 7 1/2 se se ten en conta que reduce o tamaño da cabeza.
Deste modo as súas obras gañan en lixeireza e graza, os membros son máis longos e flexibles e a musculatura menos marcada.
Leocares xa no século IV a.C., mantén a cabeza como módulo prolongando o canon ata 8 cabezas e media. Así o reflicte o Apolo Belvedere, unha figura en movemento, copia romana dun orixinal en bronce atribuído a Leocares
3- ROMA CONTINÚA O ESTUDIO DO CANON
...
Este arquitecto romano do século I a.C., só fixo unha obra pero escribiu o tratado De Architectura, 10 libros dedicados a Augusto nos que analiza tanto a parte teórica coma a parte edilicia da arquitectura.
Se xa vimos como explica a orixe das cariátides, agora imos fixarnos na súa exposición sobre a compositio, sexa de elementos arquitectónicos -basas, capiteis,...- ou sexa da figura humana. Entende por compositio a planificación dun sistema de proporcións tendo como referente un módulo, nos templos sería a súa anchura que ven dada do diámetro da columna, equivalente a un pé. Columna que por certo se constrúe a imitación do home: a basa é o pé, o fuste será o corpo e o capital equivale á cabeza.
Pero deixemos a arquitectura e vaiamos ó canon da figura humana para configurar o homo bene figuratus. Os membros do corpo son partes proporcionadas do todo e mídense por medio dunha unidade mínima -e as súas fraccións- que pode ser o palmo ou o dedo, xa que 4 palmos ou 16 dedos forman a dimensión dun pé, a unidade básica dos romanos.
A altura proporcionada é a correspondente a 24 palmos, 96 dedos ou 6 pés, pero tamén 8 cabezas, o mesmo que no canon de Lisipo, ou 10 rostros. Así dice:
Mais repercusión tivo o que denominou cuadratura do círculoCompuxo a natureza o corpo do home de sorte que o seu rostro, desde a barba ó alto da fronte e a raíz do pelo é a décima parte da súa altura. Outro tanto é a palma da man desde ó nó do pulso ata o extremo do dedo largo. Toda a cabeza desde a barba ato o alto do vértice ou cocote é a oitava parte do home. O mesmo é por detrás desde a caluga ata o alto. Desde o alto do peito ata a raíz do pelo é a sexta parte: ata o cocote a cuarta. Desde debaixo da barba ata o inferior do nariz é un terzo do rostro: todo o nariz ata o cello outro terzo, e outro desde alí ata a raíz do pelo e fin da fronte. O pé é a sexta parte da altura do corpo: o cóbado a cuarta; o peito tamén a cuarta.
Así mesmo o centro natural do corpo humano é o embigo, pois tendido o home supinamente, e abertos os brazos e as pernas, se se pon un pé do compás no embigo, e se forma un círculo co outro, tocará os extremos dos pés e das mans. O mesmo que nun círculo sucederá nun cadrado; porque se se mide desde as plantas ó cocote, e se pasa a medida transversalmente aos brazos tendidos, resultará ser a altura igual á anchura, sendo un cadrado perfecto.Círculo e cadrado representan o pensamento platónico, segundo o que o círculo simboliza o Demiúrgo -os puntos que o forman están a igual distancia do centro-, e o cadrado representa o módulo da arquitectura. Lamentablemente non temos imaxes desta proposta de Vitruvio, haberá que esperar para que posteriores tratadistas interpreten esta construción xeométrica de distintos xeitos.
Certamente as propostas de Vitruvio tiveron fonda influencia tanto na Idade Media como, especialmente, no Renacemento.
5- O MUNDO MEDIEVAL
...
A perda dos coñecementos clásicos e o teocentrismo fixeron que as reflexións teóricas escasearan nesta longa etapa e que os mestres se despreocuparan das proporcións perfectas da figura humana. A concepción simbólica da arte fai que se busque a beleza ética e non tanto a beleza estética.
Desde un románico caracterizado pola rixidez e planitude pasamos, a partir do século XII, ó gótico que alonga e estiliza as figuras ó tempo que as humaniza, pero en ningún caso se chega a establecer un módulo ou un canon, cada artista interpreta libremente as proporcións.
Reflexións teóricas sobre a beleza só as encontramos en san Agustín quen continuando coa tradición clásica a fundamenta na medida, a proporción e o ritmo.
- Villard de Honnecourt, mestre arquitecto do século XIII escribiu Livre de portraiture, unha especie de caderno de viaxe -os mestres eran itinerantes- con debuxos e explicacións de todo o que considera de interese sobre técnicas construtivas, deseños de máquinas, métodos para representar figuras humanas. Sérvese de formas xeométricas sinxelas -triángulos, cadrados, rectángulos- sen chegar a integrar un completo sistema de proporcións, aínda que se aproxima: divide a altura total en 7 partes.
Triangulación e segmentación con liñas de guía, serven tanto para as figuras estáticas como en movemento.
 |  |
Entre as súas anotación podemos ler un eloxio da xeometría e algunha anotación sobre proporcións (observa que emprega o rostro como módulo: altura de 9 rostros):
Nestas catro follas hai figuras da arte da xeometría: pero quen queira saber como se debe realizar cada unha delas, convén que se aplique moito no seu coñecemento.Pódese tomar a lonxitude do rostro e multiplicalo por nove para obter a lonxitude total da figura, multiplicala por dous para obter a súa anchura e por dous e medio para obter a anchura en caso de estar vestida.
- Cennino Cennini, no Gótico tardío da Italia de finais do Trecento, publica o que se considera o primeiro escrito de carácter didáctico sobre técnicas artísticas: O libro da arte. O texto é unha importantísima fonte de información para coñecer o modo de traballo e as técnicas empregadas nos talleres medievais. Foi, e segue a ser, un recurso para os restauradores e tamén para os falsificadores !.
Sobre a medida que debe ter un corpo de home feito perfectamente e, indica:
[...] o rostro divídese en tres partes, isto é: a cabeza, unha; a barba, a outra, do nariz á barba, a outra. Da punta do nariz ata a liña dos ollos, unha destas medidas; dunha orella la outra, o largo da cara; da barbela á papada, unha das tres medidas; a gorxa, o largo dunha medida; da forcada da garganta á parte superior do ombreiro, unha cara; do ombreiro ó cóbado, unha cara; do cóbado ó pulso, unha cara e unha das tres medidas; todo o largo da man, unha cara; do oco da garganta ó estómago, unha cara; do estómago ó embigo, unha cara; do embigo ó pube, unha cara; [...] É o home tan alto canto é de ancho de punta a punta dos seus brazos; estende os brazos ata media nádega. E todo ten de largo oito caras e dous das tres medidas.
Así pois considera a cara como módulo de medida, e a altura sería a equivalente a 8 2/3 de caras, correspondente tamén á envergadura dos seus brazos estendidos. As súas propostas están moi conectadas coas bizantinas (canon do Monte Athos).
Será a unidade de medida que igualmente seleccione Diego de Sagredo, arquitecto español que publica en 1565 Medidas do Romano, a primeira versión dialogada fora de Italia sobre Vitruvio.
6- A ITALIA DO RENACEMENTO
A Italia renacentista retomou o estudio dos sistemas de proporcións con verdadeira veneración, entendéndoas como a realización dun postulado metafísico, non como un mero procedemento técnico. Só Alberti e Leonardo adentráronse pola senda do empirismo na procura dunha antropometría verdadeiramente científica.
- Leon Battista Alberti -matemático, poeta, arquitecto, erudito,..- retoma o estudio das proporcións. En De pictura (1435) escribe sobre a necesidade de valerse da observación e a necesidade da proporción
A mesma Natureza nos puxo diante dos ollos todas as medidas do corpo humano; e así o estudoso encontrará moita utilidade na investigación das proporcións por si propio no natural.... O arquitecto Vitruvio mide o home polo pé; pero a min paréceme máis digno que todos os seus membros se suxeiten á dimensión da cabeza, ben que, segundo teño observado, en case todos os homes a lonxitude do pé é igual á que hai desde a barba ata o cumio da cabeza: polo que é necesario medir todos os demais membros por un destes dous, de modo que en toda a figura non exista membro que non corresponda ós demais en lonxitude e anchura.Posteriormente en De statua (1464), fixa un canon para facer unha estatua fundamentando empiricamente o seu sistema coa medición de múltiples modelos. Curiosamente toma como módulo o pé e non a cabeza como sinalara no texto anterior: a altura total é de 6 pés -cada pé serán 10 polgadas-. Trátase dun sistema simple pero é o primeiro do Renacemento.
Este modelo canónico de medición precisa variacións para adecuarse a casos particulares. Neste sentido alude á fábula de Zeuxis (pintor grego do século V a.C.) quen para representar a Helena de Troia pregou ás cinco doncelas máis fermosas de Crotona que lle permitiran pintar o mellor de cada unha.
 |
| Antonio Gadea, Zeuxis e as cinco virxes de Crotona, 2011 |
¿Como modificar entón o modelo? Para cambiar as proporcións crea o definitor, un instrumento de medición no que se xoga coa lonxitude do exempeda -a regla de 6 pés, subdivididos en 60 polgadas e 600 minuta-, sistema de medidas por el creado, que tiña como vantaxe empregar unidades moito mais pequena que a cabeza, o rostro ou o pé.
 | DEFINITOR Consta dun aro graduado horizontal fixado na parte máis alta da cabeza, no seu centro asenta un brazo xiratorio tamén graduado do que pende ata o chan unha plomada que rozará o lugar desexado, obtendo tres medidas: distancia desde o centro do arco ó punto de unión da plomada, ángulo marcado polo brazo xiratorio sobre o círculo graduado e distancia do punto que se desexe obter do chan. |
- Leonardo da Vinci, partindo das proporcións sinaladas por Vitruvio, elabora sobre 1490 un debuxo no que aplica os principios vitruvianos sobre as proporcións do corpo humano. Pero fixo algunha corrección como considerar o pé a sétima parte da altura.
O resultado é esta sanguina coñecida como Home de Vitruvio ou Ad Quadratum na que se representa a si mesmo espido, con dúas posicións sobreimpresas de brazos e pernas e inscrito nun círculo e nun cadrado.
Na parte superior fai referencia a Vitruvio e ó seu libro, e ninferior, debaixo da regla de módulos proporcionados -basada no cóbado, dividido en 6 partes e unha destas dividida en 4-, escribe as medidas anatómicas que no home corresponden por natureza.
Estas son as anotacións que escribe e coas que subliña a idea da pintura como ciencia cunha base matematicamente mensurable:
Igualmente estivo interesado na investigación sobre a proporción áurea que el mesmo aplicou nas súas obras, e ilustrou cos seus debuxos, como o da esquerda, o texto de Luca Pacioli De Divina Proportione.
Volvendo ás proporcións anatómicas, certo que Leonardo non foi o primeiro nin o derradeiro en levar ó papel o Home de Vitruvio, outros artistas eruditos plasmaron de xeitos semellantes os plantemaentos de Vitruvio.
- Taccola, como foi coñecido Mariano di Jacopo (1382-1453), un enxeñeiro e artista de Siena que case 70 anos antes que Leonardo, ilustrou a figura ideal.
- Tamén a ilustración de Francesco de Giorgio Martini, igualmente sienés, é anterior. Entre 1475 e 1476 durante a súa estadía en Urbino, escribiu o Tratado de arquitectura civil e militar, no que inclúe o Home de Vitruvio
Posteriores son as restantes representacións
Cos estudios de anatomía, mellorou o coñecemento do corpo humano, pero os artistas engadiron a propia idea de beleza. Así Miguel Anxo,
precursor do Barroco, rexeita a exactitude numérica das proporcións xa
que estas varían segundo a disposición e o punto de vista. As súas
figuras monumentais chegan a un canon de 8 ou incluso 11 cabezas.
Escribe:
7- DO SUR Ó NORTE: DURERO
...
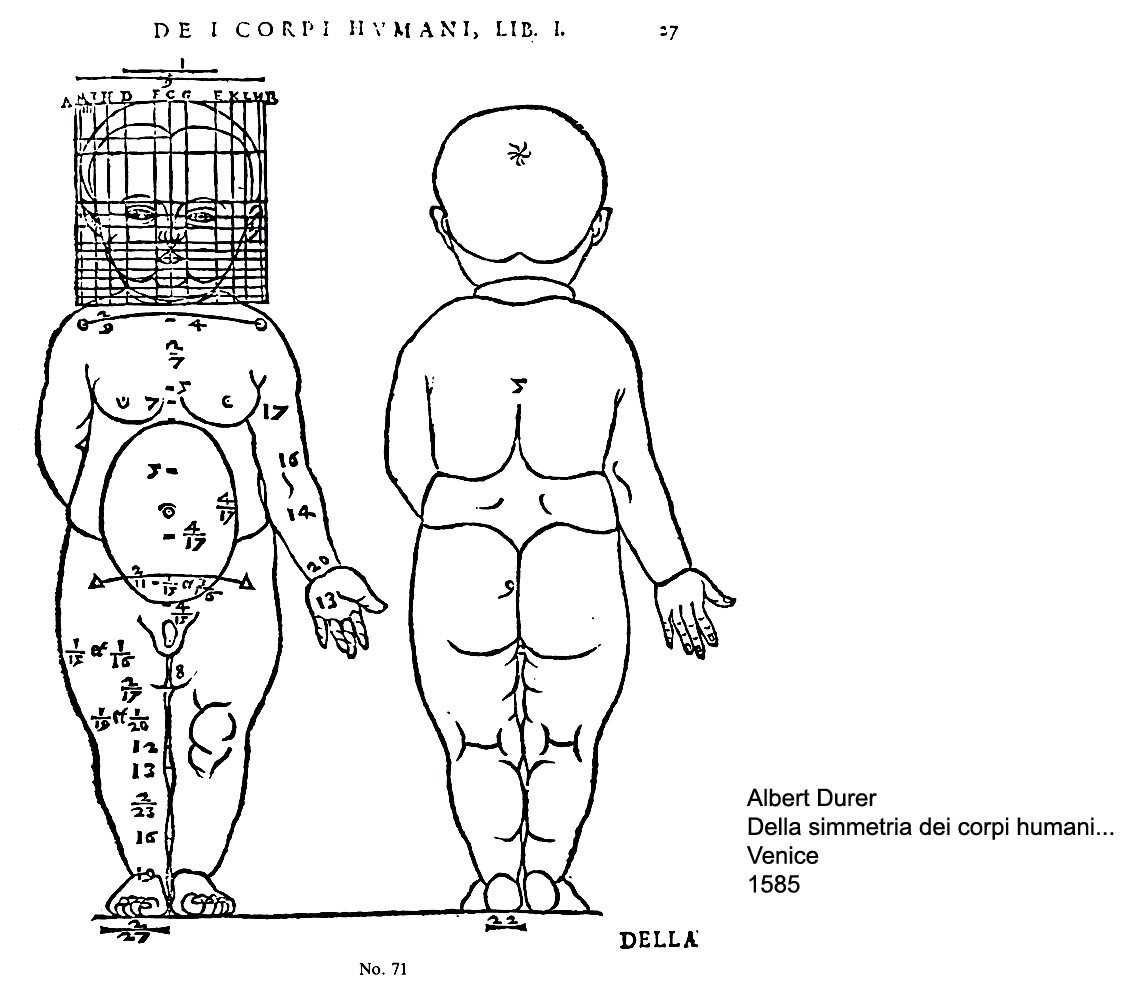
Alberto Durero, na Alemaña do século XVI, influído pola arte clásica, volveu ó estudio das proporcións que un corpo humano ha de ter para ser considerado fermoso.
Matemático, ademais de artista, reflectiu as súas reflexións en Os catro libros das proporcións humanas, publicación póstuma de 1528. Nas súas viaxes a Italia entrara en contacto cos estudos canónicos clásicos, o que o moveu a desenvolver os seus propios estudos, cos que ensinar ós xoves artistas, para os que se serviu de observacións directas de duascentas ou trescentas persoas.
A primeira das súas innovacións foi establecer que non existe un único ideal de beleza senón que a beleza pode ser acada de distintas formas e con distintas proporcións, o que o apartaba do empeño clásico de encontrar un único modelo obxectivo de proporción. Durero insiste que na arte a creatividade artística supera o dato canónico obxectivo, é dicir, hai algo máis que o puramente físico e mensurable.
Chega a establecer ata 21 posibilidades incluíndo un canon diferenciado para homes, mulleres e nenos, o que de novo é unha novidade. No primeiro libro fixa cinco tipos para homes e outros tantos para mulleres cada un cunha característica: forte, groso, fino, longo e curto. No segundo libro fixa oito tipos para os varóns e dez para mulleres, incluíndo ademais a simulación matemática precisa para traballar a figura reflectida en espellos cóncavos e espellos convexos. O obxectivo era que con eses tipos se puidera evitar a pura fealdade.
É neste segundo libro no subdivide a altura en fraccións para cada parte do corpo, extremadamente puntilloso na exactitude, chega a establecer como unidade mínima a "partícula" -trümlein- inferior a 1 milímetro.
De especial importancia é resaltar que Durero non só estudiou a figura humana en repouso, de pé, senón que tamén fixo moitos apuntes sobre a figura en movemento sevíndose de poliedros e cubos. O que neste caso lle interesaba non era a proporción senón os volumes orientados en distintas direccións: formas e espazo tridimensional. Estamos a falar de perspectiva, e o resultado dos debuxos de Durero semellan figuras cubistas.
8- SÉCULOS XIX e XX
Na parte superior fai referencia a Vitruvio e ó seu libro, e ninferior, debaixo da regla de módulos proporcionados -basada no cóbado, dividido en 6 partes e unha destas dividida en 4-, escribe as medidas anatómicas que no home corresponden por natureza.
Estas son as anotacións que escribe e coas que subliña a idea da pintura como ciencia cunha base matematicamente mensurable:
Como unidades de medida empregou, o pé, a cabeza (do cocote ó queixo) co valor de 1/8 da altura e a cara (do comezo do pelo ata o queixo) que equivale a 1/10 da altura, ambas vixentes desde os tempos de Vitruvio. O conxunto encaixa nunha cuadrícula de 10x10, equivalente cada unha a medio cóbado.
Pero introduciu algunha corrección como considerar o pé a sétima parte da altura e non a sexta como o arquitecto romano.
Por suposto que Leonardo fixo, como en tantos outros campos, as súas propias investigacións sobre as proporcións ideais. Así o vemos nas láminas que seguen coas súas anotacións e especificacións. 
Pero introduciu algunha corrección como considerar o pé a sétima parte da altura e non a sexta como o arquitecto romano.
 |
| Cuboectaedro romboidal |
Volvendo ás proporcións anatómicas, certo que Leonardo non foi o primeiro nin o derradeiro en levar ó papel o Home de Vitruvio, outros artistas eruditos plasmaron de xeitos semellantes os plantemaentos de Vitruvio.
- Taccola, como foi coñecido Mariano di Jacopo (1382-1453), un enxeñeiro e artista de Siena que case 70 anos antes que Leonardo, ilustrou a figura ideal.
- Tamén a ilustración de Francesco de Giorgio Martini, igualmente sienés, é anterior. Entre 1475 e 1476 durante a súa estadía en Urbino, escribiu o Tratado de arquitectura civil e militar, no que inclúe o Home de Vitruvio
Posteriores son as restantes representacións
 |
| Frá Giocondo, 1511 |
 |
| Cesare Cesariano, 1521 |
 |
| Carlo Urbino, 1553 |
Escribe:
É preciso ter o compás nos ollos e non na man, porque as mans obran pero o ollo xulga.
7- DO SUR Ó NORTE: DURERO
...
Alberto Durero, na Alemaña do século XVI, influído pola arte clásica, volveu ó estudio das proporcións que un corpo humano ha de ter para ser considerado fermoso.
Matemático, ademais de artista, reflectiu as súas reflexións en Os catro libros das proporcións humanas, publicación póstuma de 1528. Nas súas viaxes a Italia entrara en contacto cos estudos canónicos clásicos, o que o moveu a desenvolver os seus propios estudos, cos que ensinar ós xoves artistas, para os que se serviu de observacións directas de duascentas ou trescentas persoas.
A primeira das súas innovacións foi establecer que non existe un único ideal de beleza senón que a beleza pode ser acada de distintas formas e con distintas proporcións, o que o apartaba do empeño clásico de encontrar un único modelo obxectivo de proporción. Durero insiste que na arte a creatividade artística supera o dato canónico obxectivo, é dicir, hai algo máis que o puramente físico e mensurable.
Chega a establecer ata 21 posibilidades incluíndo un canon diferenciado para homes, mulleres e nenos, o que de novo é unha novidade. No primeiro libro fixa cinco tipos para homes e outros tantos para mulleres cada un cunha característica: forte, groso, fino, longo e curto. No segundo libro fixa oito tipos para os varóns e dez para mulleres, incluíndo ademais a simulación matemática precisa para traballar a figura reflectida en espellos cóncavos e espellos convexos. O obxectivo era que con eses tipos se puidera evitar a pura fealdade.
É neste segundo libro no subdivide a altura en fraccións para cada parte do corpo, extremadamente puntilloso na exactitude, chega a establecer como unidade mínima a "partícula" -trümlein- inferior a 1 milímetro.
 |  |
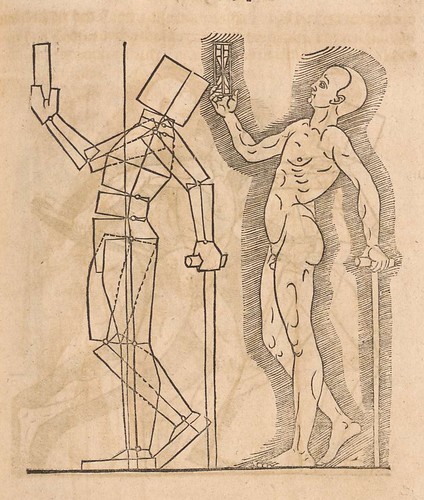8- SÉCULOS XIX e XX
Neste século XIX continuaron a desenvolverse notablemente os estudios antropométricos, abundando os realizados por médicos (Zeising, Stratz, Richter), e os referentes á proporción e o número áureo, asunto analizado noutra entrada.
Haberá que esperar ó século XX para que dous arquitectos aplicando a razón áurea á arquitectura e fixen sistemas de proporcións, como Neufert e, sobre todo, Le Corbusier.
Le Corbusier consideraba pouco eficaz o sistema métrico para construír adecuadamente edificios, habitacións e obxectos. Pero tamén buscando a estética.
Comezou o seu estudio volvendoa ás unidades de medidas clásicas: pulgada, cóbado, palmo e pé. Primeiro traballou coa altura promedio do home francés pero pronto pasou ó do home inglés que se define cun promedio de 6 pés, 1,82 m. Logo pasará a empregar o tipo latino de 1,72 m de altura.
Así chegou ó Modulor -o libro publícase en 1950-, un sistema de medidas no que cada magnitude se relaciona coas demais segundo a proporción áurea e á vez se corresponden coas medidas do corpo humano.
Desde o embigo marcas dúas escalas, azul e vermella, multiplicando e dividindo por phi obtén unha serie de Fibonacci. As dimensións da escala azul son o dobre que as da escala vermella.
Así sintetiza ó escribir:
O sistema serve tanto para os edificios coma para obxectos ou mobiliario. ¿Cantas veces temos dito: este tallo ou esta mesa non resultan cómodo?. Mira como Le Corbusier fixa as medidas idóeas nara distintas posicións.
Os mesmos principios aplicou na arquitectura: todo o edificio de Unidade de Habitación en Marsella está feito de acordo coas proporcións do módulor
Haberá que esperar ó século XX para que dous arquitectos aplicando a razón áurea á arquitectura e fixen sistemas de proporcións, como Neufert e, sobre todo, Le Corbusier.
 |
| Neufert: adecuación de mobiliario de oficinas |
Le Corbusier consideraba pouco eficaz o sistema métrico para construír adecuadamente edificios, habitacións e obxectos. Pero tamén buscando a estética.
Comezou o seu estudio volvendoa ás unidades de medidas clásicas: pulgada, cóbado, palmo e pé. Primeiro traballou coa altura promedio do home francés pero pronto pasou ó do home inglés que se define cun promedio de 6 pés, 1,82 m. Logo pasará a empregar o tipo latino de 1,72 m de altura.
Así chegou ó Modulor -o libro publícase en 1950-, un sistema de medidas no que cada magnitude se relaciona coas demais segundo a proporción áurea e á vez se corresponden coas medidas do corpo humano.
Un home co brazo levantado da ós puntos determinantes da ocupación do espazo -o pé, o plexo solar, a cabeza, a punta dos dedos estando levantado o brazo- tres intervalos que definen unha serie de seccións áureas de Fibonacci; e por outra parte a Matemática ofrece a variación máis sinxela e máis forte dun valor: o simple, o doble e as dúas seccións áureas.O Modulor parte da medida do home coa man levantada, 226 cm, e da súa metade, 113 cm, marcada na liña do embigo. Unha terceira liña horizontal no alto da cabeza danos a altura. Temos pois tres medidas: 113, 70 e 43. E todas se relacionan de acordo á proporción áurea.
Desde o embigo marcas dúas escalas, azul e vermella, multiplicando e dividindo por phi obtén unha serie de Fibonacci. As dimensións da escala azul son o dobre que as da escala vermella.
Así sintetiza ó escribir:
- Un home có brazo levantado da ós puntos determinantes da ocupación do espazo -o pé, o plexo solar, a cabeza, a punta dos dedos estado levantado o brazo- tres intervalos que definen unha serie de secións áureas de Fibocacci; e por outra parte a matemática ofrece a variación máis sinxela e máis forte dun valor: o simple, o doble e as dúas seccións áureas.
O sistema serve tanto para os edificios coma para obxectos ou mobiliario. ¿Cantas veces temos dito: este tallo ou esta mesa non resultan cómodo?. Mira como Le Corbusier fixa as medidas idóeas nara distintas posicións.
E visto todo isto, ¿que pensas?, ¿a beleza resulta da perfección?, ¿hai obxectividade no que nos gusta ou no que non?. En fin, abro a porta ó debate da beleza no mundo real.....
Como resulta difícil facer un estudio de proporcións sobre fotografías só un derradeiro planteamento: a beleza é tamén simetría (recorda os gregos). Pero en realidade non somos exactamente simétricos, no sentido actual da palabra.
Mira as imaxes de abaixo, unha está trucada para ser perfectamente simétrica -a mesma metade se repite nos dous lados-. ¿Cal che resulta máis atractiva ou suxerente: a 1 ou a 2?
 |
| Para ler a resposta pasa o rato sobre o texto de abaixo, entre os dous guións .............................. -A imaxe 1 é perfectamente simétrica, a imaxe 2 é a imaxe real na que existen certas asimetrías- |
