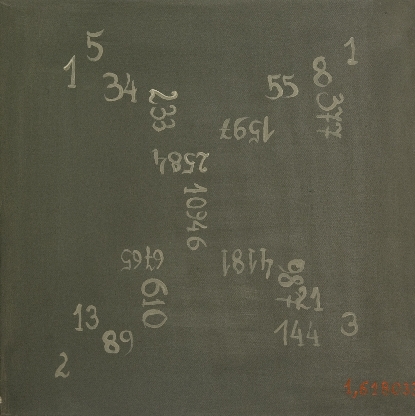¿Unha entrada de matemáticas nun blog de arte?. Pois si, tamén a arte lle debe moito ás matemáticas e, por suposto, á xeometría. ¿De que xeito?. Recordemos que xa Aristóteles na Metafísica escribiu:
Os filósofos que aseguran que as ciencias matemáticas non tratan do fermosos nin do ben están nun erro porque o fermoso é o obxecto principal do razoamento destas ciencias e das súas demostracións (...). As formas máis elevadas do fermoso son a orde, a simetría, o definido, e é así, sobre todo, donde aparecen as ciencias matemáticas. E posto que estas formas (a orde e o definido) son causas manifestas dunha multitude de efectos, é evidente que as matemáticas deben considerarse como causa do fermoso.E moito despois, Le Corbusier sinalaba:
Detrás da parede, os deuses xogan, xogan cos números cos que o universo está feito.Incluso Apollinaire escribiu no 1913:
A xeonetría é ás artes plásticas o que a gramática á arte de escribir.Así que fagamos un repaso
É unha aportación da xeometría dos pitagóricos, unha especie de sociedade relixioso-filosófica que mantiña que todo se podía reducir a números, e que Euclides (325-265 a.C.) definiu como unha relación entre segmentos. O resultado desa relación da o número phi, a letra grega en honor a Fidias.
Parte de dividir un segmento recto en dúas partes cunha característica especial: que a razón entre a parte máis larga e a menor sexa a mesma que entre a lonxitude total e a parte menor. Expresado a través de ecuacións sería como ves abaixo, e unha vez resolta da o número irracional phi.
O mesmo número se obtén na sucesión de Fibonacci, como veremos logo.
Aplicando ese número como medida de proporcións na relación entre as partes, ben sexa dun edificio ou dunha pintura, obteríase a harmonía e a beleza. Encontrámolo na arte, pero tamén na natureza ou na música.
Xa falamos dela cando estudamos a arte grega, está no Partenón ou no Dorífero, e neste post está recollido un estupendo vídeo sobre este punto.
Aplicando ese número como medida de proporcións na relación entre as partes, ben sexa dun edificio ou dunha pintura, obteríase a harmonía e a beleza. Encontrámolo na arte, pero tamén na natureza ou na música.
Xa falamos dela cando estudamos a arte grega, está no Partenón ou no Dorífero, e neste post está recollido un estupendo vídeo sobre este punto.
Pola súa calidade estética recibe a denominación de razón/proporción áurea ou divina proporción, e pensa se será recoñecida que ata Rafael Alberti, pintor ademais de poeta, lle fixo un poema recollido en Poemas del destierro.
Maruja Mallo tamén sinalou
En mi conexión con el Número Áureo y el mundo de lo Esotérico, así como con la Astronomía me conecto directamente con el concepto de Dios
1 - Rectángulo áureo é aquel no que os seus lados teñen a relación de número áureo, do mesmo xeito só é áureo aquel rectángulo que partido para obter o maior cadrado posible, da como resultado un novo rectángulo semellante, é dicir áureo igualmente.
Constitúe un deseño moi empregado no mundo cotiá desde as tarxetas de crédito ata os paquetes de cigarros pasando polos libros, pero o seu uso no mundo da arte ven de moi longo e chega ata o presente.
Fíxate a continuación como se obtén un rectángulo áureo a partir de outro.
¿Como obter o primeiro rectángulo áureo?. Para iso debemos partir dun cadrado, marcar o punto medio dun dos lados e logo trazamos un arco de circunferencia no que o radio sexa a distancia desde ese punto medio ó vértice superior. Prolongamos as liñas superior e inferior e facemos unha paralela, entón ¡voilá!, xa temos un rectángulo de proporcións perfectas.
Agora podemos continuar
a facer máis rectángulos dourados, basta trazar un cadrado a partir do
lado maior do rectángulo que temos, e así sucesivamente.
2 - Espiral áurea ou de Durero, obtense dentro dun rectángulo áureo ó unir cun arco de circunferencia os vértices opostos dos cadrados conseguendo unha espiral. Denominada de Durero quen no século XVI tomou como referentes o número áureo e a sucesión de Fibonacci. Posteriormente Descartes denominaríaa espiral logarítmica.
Aparece tanto na natureza coma na arte, incluíndo algunhas composicións de Bethooven ou de Mozart.
Certos deseños actuais empregan como base a divina proporción. Mira o deseño do logotipo e da páxina de Twitter:
3- Pentagrama, é unha estrela de cinco puntas que se pode formar a partir dun pentágono regular -o seu lado é o segmento áureo da diagonal-, está formado por dez triángulos áureos, pero tamén todos os segmentos que se forman son áureos.
Para os pitagóricos o pentagrama ou pentalfa -porque contén cinco letras alfa- era o seu símbolo de identificación, un símbolo secreto que lles permitía recoñecerse como membros do grupo. Significaba saúde e as cinco puntas simbolizarían os cinco elementos.
 |
| Miguel Anxo, Sagrada Familia |
 |
| Dalí, Leda atómica |
O Departamento de Defensa dos Estados Unidos tamén ten forma pentagonal. Construíuse despois da IIGM, ¿pensarían no significado simbólico desta forma xeométrica?. Non sabemos, pero desde logo encaixa ben o contido e o seu contenedor.
4- Triángulos áureos e outras formas áureas como un decágono ou unha estrela áurea, ou todas aquelas que serán áureas con tal de manter a relación de proporcións phi.
Por suposto que a combinación de formas áureas ás veces non resulta visible nunha primeira ollada porque detrás da imaxe do lenzo hai todo un estudio de proporcións que só resulta recoñecible cando se analizan. Mira esta iluminación de Jean Fouquet, á esquerda, e observa todas as medidas e formas xeométricas subxacentes, son todas de proporción áurea.
No 2006 o artista chinés presentou esta escultura en madeira de haunghuali baixo o nome de Divina proporción, á dereita, un icosaedro de doce caras pentagonais e vinte hexagonais realizado con técnicas tradicionais. Como veremos a fonte está en Leonardo de Vinci.
Este matemático italiano (1170-1250) chamado Leonardo de Pisa, introdutor dos números arábigos e o 0, estableceu unha sucesión infinita de números naturais no que a partir do terceiro, o seguinte se obtén da suma dos dous anteriores:
0, 1, 1, 2, 3, 5, 8,
13, 21, 34, 55, 89, 144, 233, 377, 610,...............
E curiosamente a división de dous números sucesivos, sempre o maior entre o menor, da como resultado un número que se vai aproximando a phi, é pois unha secuencia áurea.
Para sintetizar estes puntos da proporción áurea, vexamos estes tres interesantes vídeos
E un exemplo de artista que utiliza a serie numérica na súa obra. Mario Merz foi posiblemente o máis xenuíno representante da Arte Povera da Italia dos anos 60, un movemento que engloba un heteroxéneo grupo de artistas unidos polo uso de materiais pobres, o rexeitado pola sociedade de consumo, ós que da un novo significado, artístico e crítico ó tempo.
Na obra que segue, unha instalación denominada Fibonacci 1202, encontramos once fotografías en branco e negro, dez luces de neon e un transformador. As fotografías reflicten un restaurante de Turín, cada unha cun número de persoas distintas que se corresponde coas da secuencia 0-1-1-2-3-5-8-13-21-34-55. Sobre as fotografías os números correspondentes en luz de neon.
¿Ten isto algunha significación?. Para Merz é a representación dos principios universais da creación e o crecemento, así como o paso do tempo
Na imaxe seguinte, Cifras no bosque, un proxecto na cidade de Salzburgo, Merz combina dúas das súas sinais de identidade: os iglús e a sucesión de Fibonacci. Nesta caso son doce tubos de aceiro dobrados e medio escondidos entre as árbores, que soportan 21 cifras en tubos de neon dentro de caixas de cristal.
E a imaxe do lenzo O soño de Fibonacci, da artista asutríaca martina Schettina.
Pero tamén poden ser creados, aparecen moito na arte dixital e no deseño gráfico (existen programas gratuítos para xeralos, así que podes xogar a crear fractales nesta páxina). Algúns consideran que a obra de Pollock obedece a ritmos fractais, é dicir que por debaixo do caos subxace unha estrutura que se repite.
Na arte fractal, o pintor non aplica pintura sobre o lenzo senón que xera unha imaxe dixital por medio de fórmulas matemáticas e algoritmos de cor. O resultado é unha imaxe que produce emoción ó contemplala.
Algúns artistas empregaron parcialmente fractales, por exemplo Hokusai faino nos bordes das olas da súa estampa A gran ola. Na actualidade, tamén os fractais aparecen no deseño como esta mesiña de café realizada en resina.
Sabemos que os poliedros (do grego πολύς -moitas- e έδρα-cara-) son corpos xeométricos tridimensionais de caras planas, sendo cada unha das caras un polígono.
Na arte empregáronse desde sempre poliedros, por exemplo pirámides. Pero imos centrarnos nos "sólidos platónicos", os cinco poliedros regulares que ves abaixo
Son os únicos poliedros regulares porque as súas caras son polígonos regulares iguais, conteñen todo tipo de simetrías que existen nun plano -e a simetría considérase base da beleza-, e presentan unha curiosidade matemática, a fórmula de Euler: a suma do número de caras (c) e o número de vértices (v) é igual ó seu número de arestas (a) máis 2, é dicir c+v = a+2.
Se ben xa se coñecían, foron os gregos os que comezaron a interesarse por estes poliedros, sendo seguramente o primeiro Pitágoras. Empédocles asociounos cos elementos primixenios (auga - icosaedro, aire - octaedro, lume - tetraedro e terra - cubo), logo Platón relacionou o dodecaedro coa substancia da que están feitas as estrelas, substancia que se supuña distinta de calquera das presentes na terra.
No Timeo, Platón escribe:
E desde entón estes cinco poliedros reciben o nome de platónicos, denominación que mantemos na actualidade. Será despois Euclides quen realmente desenvolva un fondo estudio matemático destes poliedros describindo como construílos.
No Renacemento agroma o seu estudio entre os artistas matemáticos e os teóricos da arte, tanto polo seu valor para os estudios da perspectiva como pola súa significación simbólica.
Piero della Francesca, remata no 1485 o seu tratado sobre xeometría, Libellus de Quinque Corporibus Regularibus sobre os cinco sólidos regulares.
O tratado, igual que os outros seus non chegou a publicarse pero circulou como copias manuscritas. Gran parte do seu contido foi incorporado por estudosos posteriores, particularmente Pacioli quen no terceiro tomo de Da Divina Proportione (1509), integra o escrito por Piero. Inclúe no comezo do texto este poema adicado ós marabillosos sólidos platónicos.
E quen realiza as ilustracións é Leonardo. Para cada figura da unha versión sólida e outra oca, baseándose en figuras de madeira. O seu dominio da perspectiva fixo posible unha mellor distinción visual de todas as caras.
Recordemos que o interese de Leonardo polas matemáticas foi notable, el solicitou do duque de Sforza que trouxera a Milán a Pacioli, para aprender del, e así sucedeu de feito. Subliña o seu fervor natemático no Tratado da Pintura ó parafrasear o texto da academia platónica escribindo
..
 Durero, outra artista matemático, dedica boa parte do seu Libro IV ó estudo dos poliedros regulares e irregulares. Respecto dos primeiros, foi o primeiro na historia da xeometría que os representa no seu desenvolvemento no plano e por dúas proxeccións ortogonais sobre os planos horizontal e vertical, é dicir amósao aberto, pechado en planta e en alzado. Á dereita podes ver os seus debuxos do icosaedro.
Durero, outra artista matemático, dedica boa parte do seu Libro IV ó estudo dos poliedros regulares e irregulares. Respecto dos primeiros, foi o primeiro na historia da xeometría que os representa no seu desenvolvemento no plano e por dúas proxeccións ortogonais sobre os planos horizontal e vertical, é dicir amósao aberto, pechado en planta e en alzado. Á dereita podes ver os seus debuxos do icosaedro.
E agora vexamos exemplos da súa utilización na arte
Unha das máis curiosas pinturas cun sólido platónico, non tanto pola súa calidade pictórica, é esta Adoración da Trinidade ou A Gloria, realizada dun xeito non moi logrado no 1584 por Lucas Cambiaso no Escorial. Cambiaso, ou Luqueto como aquí se coñeceu, foi un pintor de orixe xenovesa chamado por Filipe II para decorar as bóvedas da igrexa do convento escurialense.
Resulta realmente sorprendente o modo no que as tres figuras centrais lo lenzo -Padre, Fillo e o Espírito Santo en forma de pomba- asentan sobre ese sólido platónico.
Mais, ¿por que se lle da esa preponderancia?. Certamente é un elemento inusual na iconografía, pero sen dúbida obtivo os parabéns de Filipe II que, non esquezamos,foi un estrito supervisor de todo o programa artístico do conxunto. Parece ser que neste caso, non gustou moito do resultado final do conxunto (ben abigarrado, certamente).
Tamén é verdade que o cubo encaixa ben nunha construción como esta do Escorial baseada nunha modulación cuadrangular ou cúbica, levada a cabo baixo a dirección de Herrera - autor dun texto titulado Discurso sobre a figura cúbica-, e na contorna temporal dun Renacemento que ensalza a figura cúbica como modelo de proporción. A todo isto habería que engadir un valor simbólico, o cubo significa firmeza e estabilidade, fortaleza e poder creador (dito por Alberti).
Rematamos cunha lámpada en forma de icosaedro, un deseño de Bertjan Pot.
O habitual é que todas as superficies teñan dúas caras, pero sorprendentemente a banda ou cinta de Moebius, moi importante en topoloxía, non cumpre esta premisa: é unha superficie dunha soa cara e dun só borde, unha cinta sen fin e non orientable -o percorrido comeza nunha orientación e remata na contraria-. Outra particularidade é que se a cortamos pola metade, non teremos dúas cintas senón unha con dúas voltas.
Constrúese moi facilmente: unimos os bordes dunha tira de papel rectangular, pero facendo un xiro nun deles, ¡e xa está!. Mira o vídeo. Podemos ver o seu uso case todos os días no símbolo de reciclaxe,pero seguramente as imaxes máis coñecidas sexan estas de Escher.
eeee
En esculturas e arquitecturas recoñecemos a banda con só miralas
Recentemente este proxecto de ponte foi o gañador dun concurso para a cidade chinesa de Meixi Lake, preto de Changdsa. Trátase dunha cidade de nova creación, planificada coma unha grande urbe -máis de 11 kilómetros cadrados para 180.000 habitantes-, pero ecolóxica e futurista. Realizada en aceiro, a ponte está inspirado na cinta de Moebius. Con 150 metros de largo e 24 de alto, con diferentes niveis de circulación e de vistas, a imaxe resultante adquire carácter case orgánico, de elemento vivo que sorprende e impresiona.
Ron Arad, deseñador israelí, é o pai deste sofá en polietileno rotomodelado, unha banda de Moebius para se sentar.
Este miradoiro construído preto de Rotterdam e desde o que se obteñen espléndidas vistas da cidade, tamén ten a súa inspiración na cinta de Moebius: unha cinta de aceiro con escaleiras trepa pola suave pendente para rematar por xirar e sde converter nun anel que volve ó punto de partida.
Son matrices nas que se dispoñen números enteiros consecutivos de xeito que a suma por columnas, por filas e por diagonais teña sempre o mesmo resultado, resultado que se denomina constante máxica.
Coñecidos na China desde o III milenio a. C., pasaron a outras culturas que lles atribuíron significados simbólicos relacionados coa astroloxía e coa adiviñación. Hoxe a súa construción segue a ser un interesante divertimento que se pode levar a cabo mediante fórmulas e algoritmos.
As representacións máis coñecidas na arte son as que fan Durero e Gaudí (mellor dito, neste último caso, os continuadores do seu traballo).
É unha retícula cadrada cun número determinado de elementos (números, cores, signos,..) por fila e columna (n x n) distribuidos de tal modo que cada un deses elementos apareza só unha vez en cada fila e columna sen repetir ubicación, é dicir non pode ocupar o mesmo lugar nunca. Na súa construción basta con fixar a primeira fila e logo ir rotando convintemente as restantes. Abaixo, tres exemplos de distinta orde: orde 3, orde 2 e orde 5.
Na súa orixe -século XI- otorgouselles valor esotérico igual que ós cadrados máxicos. Os sudokus son un xeito de cadrados latinos. O matemático Euler foi o primeiro en estudar seriamente estas construcións.
O pintor e deseñador gráfico de orixe suiza, Richard Paul Lohse, enmarcado no Constructivismo defensor das formas xeométricas planas, estudioso da cor, xoga en ocasións cos cadrados latinos nos seus lenzos, ás veces en celdas perfectamente regulares, outras veces deformando as celdas para convertilas en rectángulos ou modificando os tamaños da retícula, pero conservando sempre o ritmo dun cadrado latino. En ocasións van organizados en grupos de cores. Os resultados son suxerentes
 Son tres aneis entrelazados dun xeito especial: se cortas un deles, calquera, o enlace de todos desfaise.
Son tres aneis entrelazados dun xeito especial: se cortas un deles, calquera, o enlace de todos desfaise.
Denominado tamén nó borromeo, ten a súa orixe nos Borromeo, familia italiana de Milán que os empregou -desde mediados so século XV- no seu brasón como símbolo de forza e unión, pero tamén da fraxilidade se falla un só dos seus compoñentes. Parecer ser que aludía á unión de tres familias poderosas: os Sforza, os Visconti e os Borromeo.
O fractal é un obxecto semixeométrico no que a súa estrutura básica, fragmentada ou irregular, repítese a diferentes escalas.
O término -do latín fractus: fracturado- foi proposto polo matemático Benoît Mandelbrot que estudou a xeometría da rugosidade. Del toma nome o algoritmo Conxunto de Mandelbrot cuxos bordes son un fractal, de xeito que cada sucesiva imaxe é a amplición dunha sección da imaxe previa (para entendelo mellor).
bifúrcase infinitamente
ten complexidade crecente
repite a mesma estrutura (autosimilitude)
Podemos ver estruturas de fractais na natureza, como nos tres exemplos que ves debaixo, os tres seguen un patrón de crecemento fractal.
Sabemos que os poliedros (do grego πολύς -moitas- e έδρα-cara-) son corpos xeométricos tridimensionais de caras planas, sendo cada unha das caras un polígono.
Na arte empregáronse desde sempre poliedros, por exemplo pirámides. Pero imos centrarnos nos "sólidos platónicos", os cinco poliedros regulares que ves abaixo
Son os únicos poliedros regulares porque as súas caras son polígonos regulares iguais, conteñen todo tipo de simetrías que existen nun plano -e a simetría considérase base da beleza-, e presentan unha curiosidade matemática, a fórmula de Euler: a suma do número de caras (c) e o número de vértices (v) é igual ó seu número de arestas (a) máis 2, é dicir c+v = a+2.
Se ben xa se coñecían, foron os gregos os que comezaron a interesarse por estes poliedros, sendo seguramente o primeiro Pitágoras. Empédocles asociounos cos elementos primixenios (auga - icosaedro, aire - octaedro, lume - tetraedro e terra - cubo), logo Platón relacionou o dodecaedro coa substancia da que están feitas as estrelas, substancia que se supuña distinta de calquera das presentes na terra.
No Timeo, Platón escribe:
O lume está feito por tetraedros; o aire, de octaedros; a auga, de icosaedros; a terra de cubos; e como aínda é posible unha quinta forma, Deus empregou esta, o dodecaedro pentagonal, para que serva de límite ó mundo.
 |
| Euclides ensinando xeometría. Escola de Atenas, Rafael |
No Renacemento agroma o seu estudio entre os artistas matemáticos e os teóricos da arte, tanto polo seu valor para os estudios da perspectiva como pola súa significación simbólica.
Piero della Francesca, remata no 1485 o seu tratado sobre xeometría, Libellus de Quinque Corporibus Regularibus sobre os cinco sólidos regulares.
O tratado, igual que os outros seus non chegou a publicarse pero circulou como copias manuscritas. Gran parte do seu contido foi incorporado por estudosos posteriores, particularmente Pacioli quen no terceiro tomo de Da Divina Proportione (1509), integra o escrito por Piero. Inclúe no comezo do texto este poema adicado ós marabillosos sólidos platónicos.
E quen realiza as ilustracións é Leonardo. Para cada figura da unha versión sólida e outra oca, baseándose en figuras de madeira. O seu dominio da perspectiva fixo posible unha mellor distinción visual de todas as caras.
Recordemos que o interese de Leonardo polas matemáticas foi notable, el solicitou do duque de Sforza que trouxera a Milán a Pacioli, para aprender del, e así sucedeu de feito. Subliña o seu fervor natemático no Tratado da Pintura ó parafrasear o texto da academia platónica escribindo
..
Non lea os meus principios quen non sexa matemático
E agora vexamos exemplos da súa utilización na arte
Unha das máis curiosas pinturas cun sólido platónico, non tanto pola súa calidade pictórica, é esta Adoración da Trinidade ou A Gloria, realizada dun xeito non moi logrado no 1584 por Lucas Cambiaso no Escorial. Cambiaso, ou Luqueto como aquí se coñeceu, foi un pintor de orixe xenovesa chamado por Filipe II para decorar as bóvedas da igrexa do convento escurialense.
Mais, ¿por que se lle da esa preponderancia?. Certamente é un elemento inusual na iconografía, pero sen dúbida obtivo os parabéns de Filipe II que, non esquezamos,foi un estrito supervisor de todo o programa artístico do conxunto. Parece ser que neste caso, non gustou moito do resultado final do conxunto (ben abigarrado, certamente).
Tamén é verdade que o cubo encaixa ben nunha construción como esta do Escorial baseada nunha modulación cuadrangular ou cúbica, levada a cabo baixo a dirección de Herrera - autor dun texto titulado Discurso sobre a figura cúbica-, e na contorna temporal dun Renacemento que ensalza a figura cúbica como modelo de proporción. A todo isto habería que engadir un valor simbólico, o cubo significa firmeza e estabilidade, fortaleza e poder creador (dito por Alberti).
Rematamos cunha lámpada en forma de icosaedro, un deseño de Bertjan Pot.
O habitual é que todas as superficies teñan dúas caras, pero sorprendentemente a banda ou cinta de Moebius, moi importante en topoloxía, non cumpre esta premisa: é unha superficie dunha soa cara e dun só borde, unha cinta sen fin e non orientable -o percorrido comeza nunha orientación e remata na contraria-. Outra particularidade é que se a cortamos pola metade, non teremos dúas cintas senón unha con dúas voltas.
Constrúese moi facilmente: unimos os bordes dunha tira de papel rectangular, pero facendo un xiro nun deles, ¡e xa está!. Mira o vídeo. Podemos ver o seu uso case todos os días no símbolo de reciclaxe,pero seguramente as imaxes máis coñecidas sexan estas de Escher.
eeee
Recentemente este proxecto de ponte foi o gañador dun concurso para a cidade chinesa de Meixi Lake, preto de Changdsa. Trátase dunha cidade de nova creación, planificada coma unha grande urbe -máis de 11 kilómetros cadrados para 180.000 habitantes-, pero ecolóxica e futurista. Realizada en aceiro, a ponte está inspirado na cinta de Moebius. Con 150 metros de largo e 24 de alto, con diferentes niveis de circulación e de vistas, a imaxe resultante adquire carácter case orgánico, de elemento vivo que sorprende e impresiona.
Son matrices nas que se dispoñen números enteiros consecutivos de xeito que a suma por columnas, por filas e por diagonais teña sempre o mesmo resultado, resultado que se denomina constante máxica.
Coñecidos na China desde o III milenio a. C., pasaron a outras culturas que lles atribuíron significados simbólicos relacionados coa astroloxía e coa adiviñación. Hoxe a súa construción segue a ser un interesante divertimento que se pode levar a cabo mediante fórmulas e algoritmos.
As representacións máis coñecidas na arte son as que fan Durero e Gaudí (mellor dito, neste último caso, os continuadores do seu traballo).
É unha retícula cadrada cun número determinado de elementos (números, cores, signos,..) por fila e columna (n x n) distribuidos de tal modo que cada un deses elementos apareza só unha vez en cada fila e columna sen repetir ubicación, é dicir non pode ocupar o mesmo lugar nunca. Na súa construción basta con fixar a primeira fila e logo ir rotando convintemente as restantes. Abaixo, tres exemplos de distinta orde: orde 3, orde 2 e orde 5.
Na súa orixe -século XI- otorgouselles valor esotérico igual que ós cadrados máxicos. Os sudokus son un xeito de cadrados latinos. O matemático Euler foi o primeiro en estudar seriamente estas construcións.
O pintor e deseñador gráfico de orixe suiza, Richard Paul Lohse, enmarcado no Constructivismo defensor das formas xeométricas planas, estudioso da cor, xoga en ocasións cos cadrados latinos nos seus lenzos, ás veces en celdas perfectamente regulares, outras veces deformando as celdas para convertilas en rectángulos ou modificando os tamaños da retícula, pero conservando sempre o ritmo dun cadrado latino. En ocasións van organizados en grupos de cores. Os resultados son suxerentes
 Son tres aneis entrelazados dun xeito especial: se cortas un deles, calquera, o enlace de todos desfaise.
Son tres aneis entrelazados dun xeito especial: se cortas un deles, calquera, o enlace de todos desfaise.Denominado tamén nó borromeo, ten a súa orixe nos Borromeo, familia italiana de Milán que os empregou -desde mediados so século XV- no seu brasón como símbolo de forza e unión, pero tamén da fraxilidade se falla un só dos seus compoñentes. Parecer ser que aludía á unión de tres familias poderosas: os Sforza, os Visconti e os Borromeo.
A propiedade matemática desta unión coñécese como brunniana –polo matemático alemán Hermann Brunn (1862-1939)-, que foi o primeiro en estudala e demostrar que realmente é imposible construír este nó sen deformar os aneis. Son importantes nas teorías de nós e na topoloxía.
Na arte, osa tres aneis ou variacións sobre eles, encontrámolos en formulacións e significacións diversas como podes ver a continuación: no sepulcro de Miguel Anxo, no templete funerario da Capela Ruccelai, nos debuxos da túnica de Palas e o centauro de Botticelli, en alusión aos Medici, en relevos e esculturas, ou en logos de diferentes empresas e institucións.
Os frisos son elementos ornamentais, unha franxa horizontalmente delimitada por dúas rectas paralelas, empregados a miúdo na arquitectura, ben sexa con representacións figuradas ou con motivos xeométricos que se repiten ó longo desa franxa por translación.
A formación dun friso prodúcese polo movemento da figura no plano, conservando o seu tamaño (isometría).
Pero, ¿cales son os movementos, transformacións, que se poden realizar no plano?. Hai as tres posibilidades que ves abaixo (sen entrar en profundidades matemáticas)
| Traslación A figura desprázase nunha única dirección | |
| Rotación ou xiro A figura rota respecto dun punto fixo, o centro de rotación | |
| Reflexión ou simetría A figura voltea a modo de expello en relación a un eixo de simetría |
|
 |
| Diferentes deseños en frisos dos alicatados nazaríes |
 |
| Frisos ornamentais na cerámcia grega do período xeométrico |
Demos un paso adiante, no lugar dun friso imos recubrir un espazo, sexa o chan, a parede ou o teito, é dicir imos facer un mosaico (xa temos visto a orixe, a evolución e modo de realizar mosaicos), mais non con teselas irregulares senón con figuras xeométricas.
Hai que cubrir toda a superficie con polígonos iguais -non valen tamaños distintos-, o patrón creado ha de cumprir tres condicións:
Fronte ás configuracións periódicas, as aperiódicas caracterízanse porque ó voltealas non coincide có orixinal xa que o seu deseño non se forma pola translación regular das pezas. Existen moitas pezas para formar este tipo de mosaicos, as mais coñecidas son as dúas de Penrose obtidas a partir dun rombo como ves na imaxe inferior.
A arte islámica, e particularmente a arte nazarí, amosa os mellores exemplos de mosaicos xeométricos periódicos irregulares en creacións ben orixinais. Para os musulmáns foi case unha necesidade xogar coa xeometría posto que a relixión prohibe as representacións figurativas.
Tan só na Alhambra encontranse 17 modelos combinatorios no conxunto de mosaicos. As pezas cránse por deformación de poligonos regulares, como triángulos ou cadrados, para logo engadir traslacións, xiros e distintas simetrías. Vexamos algúns destes deseños (observa que a figura resultante sempre conserva a mesma área que o polígono inicial)
Animacións aqui
Lichtenstein, mais coñecido polas súas pinturas de puntos, tamén traballo con estruturas modulares, como nestas obras
Menos frecuentes son as teselacións na arquitectura, pero hai algunha na arquitectura contemporánea
Escher, artista holandés, amosou desde sempre un grande interese polas matemáticas e os problemas de xeometría. Sendo mozo, os seus adiñeraidos pais custearónlle unha viaxa por España e Italia como remedio contra as súas tendencias depresivas. O seu paso pola Alhambra e o Generalife en Granada e pola Mesquita de Córdoba, xunto cos estudios de Poincaré, levaronno a unha idea: teselar unha superficie coa idea de infinito.
Pero as obras de Escher mais coñecidas son aquelas construídas por deformación isométrica de polígonos con compensación de áreas (de novo, a Alhambra). O resultado son sorprendentes mosaicos de lagartos, aves, rás, cabaleiros,.... xerados a partir de polígonos con traslacións e xiros. O resultado son sorprendentes mosaicos de lagartos, aves, rás, cabaleiros,.... xerados a partir de polígonos con traslacións e xiros.
O exemplo do lagarto podes velo nesta animación.
Algunhas obras de Escher deste mesmo tipo
Non deixes de ollar Metamorfose I e Metamorfose II, unha delicia que se pode apreciar no seu gran formato de 4 metros de longo neses enlaces (ampliar e deslizar).
E como el mesmo dicía
Abaixo, unha cascada na que auga en movimento perpetuo contra da gravidade, e un Belveder no que non queda claro quen está dentro e quén fora
Outra pintora, representante do Op-Art, Bridget Riley centrou parte da súa obra en lograr con formas xeométricas teseladas sensacións de movemento, como nestas dúas: Cataract 3 (¿que mareo!) e Britannia.
- que as teselas non se puperpoñan
- que non queden espazos baleiros entre elas
- que a suma dos ángulos coincidentes no vértice sexa 360º
Fronte ás configuracións periódicas, as aperiódicas caracterízanse porque ó voltealas non coincide có orixinal xa que o seu deseño non se forma pola translación regular das pezas. Existen moitas pezas para formar este tipo de mosaicos, as mais coñecidas son as dúas de Penrose obtidas a partir dun rombo como ves na imaxe inferior.
A arte islámica, e particularmente a arte nazarí, amosa os mellores exemplos de mosaicos xeométricos periódicos irregulares en creacións ben orixinais. Para os musulmáns foi case unha necesidade xogar coa xeometría posto que a relixión prohibe as representacións figurativas.
Tan só na Alhambra encontranse 17 modelos combinatorios no conxunto de mosaicos. As pezas cránse por deformación de poligonos regulares, como triángulos ou cadrados, para logo engadir traslacións, xiros e distintas simetrías. Vexamos algúns destes deseños (observa que a figura resultante sempre conserva a mesma área que o polígono inicial)
Animacións aqui
Lichtenstein, mais coñecido polas súas pinturas de puntos, tamén traballo con estruturas modulares, como nestas obras
Menos frecuentes son as teselacións na arquitectura, pero hai algunha na arquitectura contemporánea
 |
| Melburne, Federation Square |
 |
| Londres, Museo Británico |
 |
| Londres, Ravensbourne College |
 |
| Pirámide do Louvre |
Escher, artista holandés, amosou desde sempre un grande interese polas matemáticas e os problemas de xeometría. Sendo mozo, os seus adiñeraidos pais custearónlle unha viaxa por España e Italia como remedio contra as súas tendencias depresivas. O seu paso pola Alhambra e o Generalife en Granada e pola Mesquita de Córdoba, xunto cos estudios de Poincaré, levaronno a unha idea: teselar unha superficie coa idea de infinito.
A solución foi o plano hiperbólico, non euclidiano, no que as teselas manteñen a forma pero reducen regularmente o tamaño para dar sensación de infinito no borde.
Anxos e demos, Escher | Disco hiperbólico de Poincaré |
Pero as obras de Escher mais coñecidas son aquelas construídas por deformación isométrica de polígonos con compensación de áreas (de novo, a Alhambra). O resultado son sorprendentes mosaicos de lagartos, aves, rás, cabaleiros,.... xerados a partir de polígonos con traslacións e xiros. O resultado son sorprendentes mosaicos de lagartos, aves, rás, cabaleiros,.... xerados a partir de polígonos con traslacións e xiros.
O exemplo do lagarto podes velo nesta animación.
Algunhas obras de Escher deste mesmo tipo
 |
| Ceo e auga. Xoga tamén coa percepción de figura-fondo. Ver vídeo |
| Día e noite, coa dualidade esquerda-dereita |
 |
| Réptiles. Desde as teselas do plano, o reptil pasa á terceira dimensión para tras resoplar no dodecaedro platónico voltar ó plano |
Non deixes de ollar Metamorfose I e Metamorfose II, unha delicia que se pode apreciar no seu gran formato de 4 metros de longo neses enlaces (ampliar e deslizar).
E como el mesmo dicía
O meu traballo é un xogo, .... Un xogo moi serioxogou coa perspectiva en figuras imposibles e co efecto Droste (unha imaxe inclúe dentro de si mesma a mesma imaxe a menor escala, e esta outra igual a menor escala,.... e asi sucesivamente. Vémolo por exemplo nos botes de Royal).
Abaixo, unha cascada na que auga en movimento perpetuo contra da gravidade, e un Belveder no que non queda claro quen está dentro e quén fora
| Galería de grabados, aplicando o efecto Droste.Na esquerda, un home mira un cadroque representa unha cidade costeira- Senglea en Malta-, onde hai unha galería de cadros,.... Parece ser que a imaxe orixinal, aparece repetida 256 veces. Para entendelo mira o vídeo |
Outra pintora, representante do Op-Art, Bridget Riley centrou parte da súa obra en lograr con formas xeométricas teseladas sensacións de movemento, como nestas dúas: Cataract 3 (¿que mareo!) e Britannia.